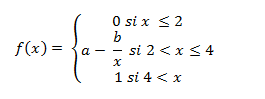Déterminer a et b pour que f soit
continue partout.
2) Montrer que l'équation :
admet exactement une solution dans [0, 1].
3) Déterminer les intervalles de
concavité et de convexité ainsi que les points d'inflexion , s'ils existent.
Exercice 2 :
1) donner le développement limité à
l'ordre 3 au voisinage de 0 de la fonction .
2) Déduire le développement limité à
l'ordre 3 au voisinage de 1 de la fonction:
Exercice 3:
Calculer les intégrales suivantes:
Exercice 4:
On considère la fonction définie par:
f(x,y)= xy
1) Déterminer le gradient de f et sa
matrice Hessiene.
2) Déterminer les extremums de la
fonction f sous la contrainte x²+y²= 2.
Correction examen analyse mathématique :
 |
| Page 1 Exam analyse mathématique s1 |
 |
| Page 2: analyse mathématique s1 |
 |
| Page 3 analyse mathématique s1 |
 |
| Page 4 analyse mathématique s1 |
 |
| Page 5 analyse mathématique s1 fsjes |
 |
| Page 6: analyse mathématique s1 fsjes économie |
admet exactement une solution dans [0, 1].
